跳到主要内容

1 篇博文 含有标签「向量」

查看所有标签

闭环的最后一步

我们在上一章讲了 Tokenization，它把单词变成了数字 ID（比如 Cat -> 673）。 但这里有一个巨大的问题： ID 673 (Cat) 和 ID 674 (Car) 在数字上只差 1，但在意义上差了十万八千里。 而 ID 673 (Cat) 和 ID 8912 (Dog) 数字差很远，意义上却很近。

如果直接把这些整数 ID 喂给 Transformer，它会疯掉——因为它找不到规律。 这就是 Embedding (嵌入层) 登场的地方。

1. 什么是 Embedding？​

简单说，就是把字典里的每一个 ID，映射到一个高维空间里的坐标 (Vector)。

想象你走进了一家巨大的无人超市。

  • Token ID 就像是商品的条形码（无意义的数字）。
  • Embedding 就像是商品在超市里的具体位置坐标 (货架3, 层数2, 左侧10米)。

在这个“语义超市”里，摆放是有规律的：

  • 🍎 苹果旁边一定是 🍌 香蕉（水果区）。
  • 🧴虽然洗发水瓶子形状像饮料，但它离苹果很远（日化区）。

Embedding 就是让 AI 即使不认识字，只要看坐标，就知道“苹果”和“香蕉”是亲戚。

2. 只有坐标，没有魔法​

在数学上，Token 变成了一个长长的浮点数列表（通常是 768 维、1536 维甚至更多）。

# 'Cat' 的 Embedding 向量 (简化版)
[0.12, -0.45, 0.88, ..., 0.03]

每一维数字代表什么？ 没有人确切知道。但在概念上，你可以想象：

  • 第 1 维代表“是否是生物”
  • 第 2 维代表“像不像动物”
  • 第 3 维代表“高贵程度”
  • ...

当模型训练完成后，神奇的事情发生了：

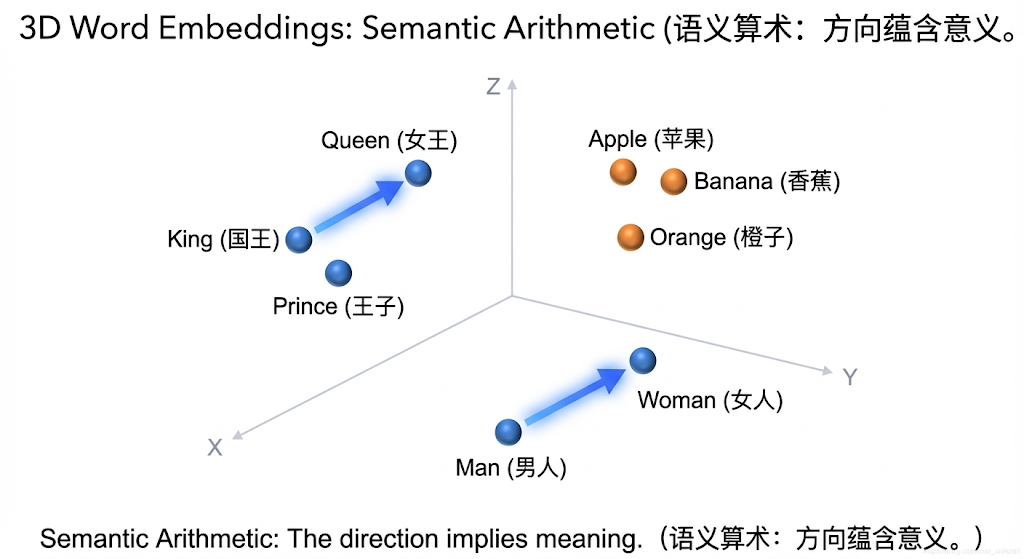
经典的“国王与王后”算术题​

如果在向量空间里做减法：

King⃗−Man⃗+Woman⃗≈Queen⃗\vec{King} - \vec{Man} + \vec{Woman} \approx \vec{Queen}

这意味着：在这个空间里，“性别”是一个固定的方向。 把“国王”身上的“男性属性”减掉，加上“女性属性”，它就自动飞到了“王后”的坐标点。

这就是 AI “理解”意义的方式：意义就是空间关系。

  • image-20260203172310732

3. 余弦相似度 (Cosine Similarity)​

既然变成了坐标，我们就可以算距离。 在 AI 里，我们通常不算直线距离（欧氏距离），而是算 夹角（余弦相似度）。

  • 方向一致（夹角 0 度） = 意思完全一样 (1.0)
  • 方向垂直（夹角 90 度） = 毫无关系 (0.0)
  • 方向相反（夹角 180 度） = 意思完全相反 (-1.0)

这就是为什么 RAG（知识库问答）能找到你想要的文档。 它不是在搜关键词，而是在高维空间里找离你问题坐标最近的那段话。

为什么不用欧氏距离？​

你可能会问，两点之间不应该算直线距离（欧氏距离 Euclidean Distance）吗？ 确实有三种常见的算距离方法：

  1. 欧氏距离 (Euclidean)：拉尺子量距离。
    • 缺点：它对“长短”敏感。如果一篇短文章和一篇长文章内容一样，只是重复了一遍，它们的向量方向一样，但长度不同，欧氏距离会认为它们差别很大。
  2. 点积 (Dot Product)：向量相乘。
    • 特点：考虑了长度。经常用在 Transformer 内部（Attention 里的 QKTQK^T 就是点积），因为那里需要保留“强度”信息。
  3. 余弦相似度 (Cosine Similarity)：只看方向，不管长度。
    • 最常用：在判断语义时，我们只关心“主题是否一致”（方向），不关心“废话多少”（长度）。所以 RAG 基本上都用这个。
简单的直觉
  • 欧氏距离：看谁离我最近（空间距离）。
  • 点积：看谁投影最强（方向一致 + 自身强大）。
  • 余弦相似度：看谁跟我长得最像（方向一致）。

4. 总结：第一层通关！​

至此，基础理论层 (Level 1) 的拼图终于完整了：

  1. 机器学习：确立了“从数据中找规律”的范式。
  2. 深度学习：造出了能拟合万物的“大脑”。
  3. CNN：给大脑装上了“眼睛”（局部特征）。
  4. Transformer：给大脑装上了“注意力”（全局关联）。
  5. Tokenization：把人类语言切碎成“数字 ID”。
  6. Embedding：把“数字 ID”变成有意义的“空间坐标”。

有了这 6 块基石，你已经可以自信地面对任何 AI 术语了。

下一章预告： 理论储备完毕，工程师们，拔剑吧。 我们要进入 【第二层：实现层】。 第一站：既然通用模型已经这么强了，我们还需要训练自己的模型吗？Fine-tuning 和 Prompt 的边界到底在哪里？

下一章: 模型训练与微调

ai学习embedding向量rag阅读需 5 分钟